THIS PART IS A BRIEF SOJOURN TO ENLARGE THE SPACE OF OUR OWN ENVELOPES TO SHOW IT CAN BE DONE, BY ACQUIRING KNOWLEDGE OF THE TESSERACT AS AN EXAMPLE, THE KNOWLEDGE OF WHICH WAS OFTEN THOUGHT TO BE BEYOND OUR KEN.
The first section of this paper concerns tesseracts (hyper cubes), of the fourth dimension. At the beginning of the 21st century, there was no coverage at all within GOOGLE regarding what such a fourth dimension object might look like. So I obtained a November 2004 copyright in an attempt to offer some clarity to the situation. And that explanation is included in this paper. Anyone else may feel free to use my writings for other papers, subject to citing where their data originated. This section has been described as being somewhat “boring”. But it is necessary in order to explain my belief that what has been thought by many to be an area next to impossible to comprehend, is within the boundaries of our mental capabilities, and therefore possible to “comprehend”.. And in understanding, the space of our envelope is enlarged. In other words, it is possible to both explain and comprehend some pretty wild stuff thought to be beyond us three dimensional mortals. And with that comprehension it will then be easier to grasp and accept the subject matter with which we will be dealing in the remainder of the paper.
So, our first goal is to describe how a four dimensional object, in this case a tesseract (hyper cube), can be explained and understood. BUT, while we may understand the object, we cannot visually see such a four dimensional object in our minds eye. However, once we have logically proved the point that the fourth dimension can exist and be logically explained, it will be easier to pass on to other considerations which are seemingly inconceivable, but which we will attempt to explain by the same logic.
Some time ago, a friend of mine asked if I would provide him with information concerning a tesseract. At the time I had been teaching about these curious objects for over 25 years to high school honor students. It was part of a half-semester course on cosmological theory; a course which we hoped would encourage them to think deeply and logically. During all that time I never bothered to put anything down in writing, except for a brief recap once or twice. One of the reasons I had not done so was because I tend to be somewhat lazy, and if I can remember something, why bother to put it down. But this was a request from a friend whom I could not deny.
Obviously I am responsible for any error in the original, often edited, paper, (and, as it has turned out, later edited writings in that paper also). As a result, it has been frequently necessary to correct my thinking, this being the sixth rewrite.. Ergo, I most humbly apologize in advance for any erroneous explanations still remaining.
We are now going to attempt to explain, to the best of our ability via the written word, an object of the fourth dimension. This paper is not meant to be a panacea for anything. It will not solve world hunger, bring universal peace, or hail the coming of a messiah for any religion. The only thing this paper concerning tesseracts and the understanding thereof is good for is as a mental exercise. But that may be a good enough end in itself.
In the process of everyday living we sometimes become involved in such minutia that we become bogged down with the unimportant to the point where the important seems to be unreachable, just beyond our fingertips. We know it is there for us to grasp, but it seems to be just beyond our ability to comprehend. A mental exercise such as that upon which we are about to embark can sometimes purge our thinking process. And often, after such an exercise, we will find that many of the cobwebs which had been clouding our thinking, to the point of making the understanding of our goal very obscure, have been cleared away. We may find that we can see more clearly that final “THOUGHT” or thought process which had been eluding us previously. With that in mind as to the why of this paper, let us begin. Let’s start with something which, I think, most will agree to. Later we will refer to something which will lead to more disagreement.
So now, let’s dig a little deeper into “cosmological truth”, and in this case, how it can help us to understand other dimensions. We have already dealt with the “cosmological constant” and later we will deal more with it. But our attention now goes to the cosmological truth which is mathematics. As the purpose of this paper is to use “logic” as much as possible to reach any of our conclusions, thus we will do so in our attempt to understand something about the fourth dimension. We will be using progressive mathematics, going through one, two, and three dimensions, as they are determined to exist by progressive math, on the way to understanding a bit of the fourth dimension. As an example of what we mean by “progressive mathematics, we have the following example: 2, 4, 6, 8, or 2, 4, 8, 16. It will be noted that this is very simple stuff. You don’t want to try to read, nor I to write, one of those papers with so much mathematics involved, logic or not, that you can’t even begin to understand the first page, let alone the entire concept the writer is trying to impart. The great majority of us are not highly educated enough to understand, and we can just sit and observe with envy what the person standing before us is trying so hard to explain. However, there is one progressive mathematical concept for which I must apologize. It is involved to the point where I am not sure I can explain it to the reader’s satisfaction. It has to do with the edges of objects. If, when reaching that point, my abilities have left you in a quagmire, please feel free to utter expletives, and just pass on.
When we speak of one, two, three, or four dimensions at this point, we are referring to one, two, three, and four dimensional universes. In no dimensions there is a SINGULARITY with no direction discernible to the outside observer, since he, as an outside observer, cannot, in any manner, detect the singularity. (At this point we must be what might seem to be repetitive to the reader.—A singularity is something which exists only unto itself. It can detect nothing outside itself and nothing outside itself can detect it. To the inhabitant of a singularity, their inside universe would appear to have no boundaries, It would seem infinite. [Our universe is a singularity, being observable only to the occupants inside it.])
At this point we will start our description of a tesseract in our effort to show that a fourth dimensional object can be understood, if not be visualized. To do so we will mainly use mathematical progression.
In one dimension there is length, consisting of forward and back. (Ignore those who insist there is another dimension because the length (road to them) must have depth. They are trying to interpret everything from the viewpoint of a three dimensional creature, and not from the viewpoint of the creature of that universe. i.e. you must interpret a one dimensional universe from the viewpoint of a one dimensional creature.
In two dimensions you add width, consisting of right and left.
In three dimensions you add height, consisting of up and down.
In four dimensions you add yuk, consisting of yik and yak. (Yuk, yik, and yak are names I gave to this fourth dimensional direction in my original paper on tesseracts, dated November 2004. Not all science has to be serious, and, this is easy to remember.
(A) In one dimension there is a line with length, consisting of forward and back..In two dimensions there is a square made by adding width, consisting of right and left.
In three dimensions there is a cube made by adding height, consisting of up and down.
In four dimensions there is a tesseract made by adding yuk, consisting of yik and yak. (tesseract is the name now given by the dictionary to this fourth dimensional object. It is also called a hypercube.)
(B) In a one dimension line there are two corners. (The ends of the line are corners, strange as it sounds. One corner at each point where the direction goes from forward to backward, or vice versa. The line has no width or height which the inhabitants of the universe can discern.) (The presence of width or height would indicate a second dimension.)
- In a two dimension square there are four corners.
- In a three dimension cube there are eight corners.
- In a four dimension tesseract there are 16 corners.
(C) In a one dimension line there are two sides.(The finite line has two sides, one going forward to one corner and the other going back to the other corner, and since there is no right or left, both lines are on top of each other by our standards, but by their standards they can’t be on top of each other because that implies the line has width or height, which in one dimension it can’t, strange as it sounds.)
- In a two dimension square there are four sides.
- In a three dimension cube there are six sides.
- In a four dimension tesseract there are eight sides.
- A one dimension line makes up one side of a two dimension square.
- A two dimension square makes up one side of a three dimension cube.
- A three dimension cube makes up one side of a four dimension tesseract. So, the side of a tesseract is actually a cube.
(E) Take a one dimension line and lay it down as a base. Next, take two more one dimension base lines and stick them straight up from each end of the laid down base line like pillars. Now get another one dimension line exactly the same as the base line and use it as a cap connecting the tops of the two pillars. You have now completed a two dimension square.
And that MUST MEAN (as we previously stated) that a three dimension cube makes up one side of a four dimension tesseract, and also makes up the cap and base.
A three dimension cube makes up one side of our four dimension tesseract (Try doing that in your wildest nightmare! It is possible for us to figure this out because we have figured out the makeup of a tesseract, BUT, we cannot visualize it since we cannot visualize the fourth dimension. Don’t try to figure it out, you will go nuts.)
If after looking at the following paragraph you are thinking “what the *^$#@”? Don’t get shook. It is only a paragraph to lead us into how we are able to make a drawing of some aspect of a four dimensional object.
(A shadow is always one dimension less than what is creating it. So a three dimension object creates a two dimension shadow; a two dimension object creates a one dimension shadow, AND a four dimension object creates a three dimension shadow. (Believe it or not.)
AND we can make a two dimension drawing of a three dimension object such as a two dimension drawing of a three dimension box. That means we can make a two dimension drawing of a three dimension shadow of a fourth dimension object. Ergo, we can have a two dimension drawing of a three dimension shadow of a fourth dimension tesseract.
The following explains the previous information. Aspirin may help. But before you want to pull your hair, or my hair, which is already mostly gone, remember we are doing this only to show that a shadow is one dimension less that the object creating it. The experiment has no other purpose.
(F) The following is impossible because of lack of dimensions as we know them to exist in our universe. I only include this as a lead-in to a two dimension example. A transparent one dimension line (having no width or height) with a one dimension light source, and that light source is shining head on that one dimension line (the lens is as big as the end of the one dimension line in front of it, in other words, no lens by our standards, because we are saying that all the lens in these examples must be of the same dimension as the object in front of it. And in this case (a lens shining head on a one dimension object, there is no up or down in that one dimension line and there is no right or left, so for our purpose, there can be no lens. {get used to that phrase, we will use it a few more times}) with neither the lens or the object having width or height , and impossible to do) would yield a no dimension, nonexistent shadow behind the other end of the line. (Don’t be concerned about trying to picture a one dimension line with no width or height, so when you attempt to take that one dimension light source and shine it head on down the line, from one end to the other, there is no shadow at the end since you would need height and width on that line to make it cast a shadow. We can picture a two dimension universe somewhat, but going back to a one dimension universe and trying to picture it is much more difficult.)
A transparent two dimension square lying flat on the table has no depth because it has only two dimensions, length and width., and then we take a two dimension light source which cannot be seen by us either, which is shining fully head on to the side of the square, (of course the “side” does not exist) but which has a lens as wide as the square lying in front of it, (again impossible to do since the lens would have no height) would yield a one dimension shadow behind the square consisting of a line only, with no height. Again impossible for us to comprehend, but don’t curse yet.
A transparent three dimension cube with a three dimension light source in the shape of one of the sides of the cube (having length and height), and then shining that lens head on would yield a two dimension shadow on the wall behind the cube in the shape of a two dimension square (or circle or whatever).
A transparent four dimension tesseract with a four dimension light source in the shape of one of the sides of the tesseract (in other words, in the shape of a cube [don’t try to figure it out]) and then shining head on would yield a three dimension shadow behind the tesseract in the shape of a three dimension cube. And voila, look at what we can do. We can make a two dimension drawing of a three dimension shadow of a four dimension tesseract, because,,, we have created a TWO dimension shadow, and we can make two dimension drawings on a piece of paper. And we now have part of an idea of what a four dimension object looks like.
(G) Forget the one dimension explanation in this example; it is too difficult for a simple mind, like mine, to explain, so we just move on to two dimensions.
A two dimension creature standing to the side of a one dimension line (which would be impossible to do) can see both sides of the one dimension line and that line is the same as one side of his square) The two dimension creature can see both sides and corners of the one dimension’s entire line
(We have done the following before.) Now, stand the two dimension square on edge, and the three dimension creature standing to the side of it sees the two dimension ( Again, no cursing, just read on.) square as one complete side of his three dimension cube. The two dimension creature is not capable of seeing his entire square as the three dimension creature can.
The three dimension creature has what the two dimension creature would consider to be surround vision. He has surround vision, as do the one dimensional creature and the two dimensional creature in the previous explanation.
That means the fourth dimension creature would seem to have surround vision in our world, being able to see all six sides of our cube at once. How does that grab you?
(H) A one dimension creature can see one side of his two sided finite line at once by standing at corner. (remember, by our standards there is only one line, but by his standards there are two lines, one coming and one going. By our standards the two lines appear to be in the same place, but not so to him, because neither width nor height exist in his universe.)
⦁ A two dimension creature can see two sides of his four-sided square at once if he stands at one corner.
⦁ A three dimension creature can see three sides of his six-sided cube at once if he stands at one corner.
⦁ A four dimension creature can see four sides of his eight-sided tesseract at once if he stands at one corner. This meaning he can see all six sides of the cube at once, again inferring some type of what to us would be surround vision.
⦁ Actually, it doesn’t work that way. It just makes a neat argumentative point to fool around with. In reality, each dimensional observer would not see the object at all since to him in order to exist for his vision, the target object must have the same number and kinds of dimensions as he/she does. And since one universe cannot look thru empty space to another universe, both being singularities,, they could not see each other.
(9) There is one line leading into the corner of the one dimensional line.
There are two lines leading into each corner of the two dimensional square.
There are three lines leading into each corner of the three dimensional cube.
There are four lines leading into each corner of the four dimensional tesseract.
And naturally in the fourth dimension they will have a fourth dimensional light source, which would in some fashion be different from our three dimensional light sources. Picture this if you will: a transparent three dimensional cube being shined upon one of its faces by a light source with a .lens having the same size and shape as the face of the cube itself. (That could be a small sized flashlight with a square lens shining upon a transparent die.)
The resulting shadow on the wall behind, assuming we have outlined all the edges of our transparent die in dark color, would be a box in a box connected at the corners. The front of the die would be the big box and the back of the die would be the little box, and the little box inside the big box would be connected to each other at the four corners.(This all sounds like whatever, even though it is fact. If you have to put too much thought into it, just forget it. It’s not that important, except to know that a shadow is one dimension less than what is creating it. It is possible, and many have made a drawing of this on the internet.)
SHOULD YOU NOT DESIRE TO INVOLVE YOURSELF TO THE POINT OF INSANITY, JUST MOVE ON TO THE DIAGRAMS, AND THEN TO PART II
Now let’s try something similar with the tesseract and a fourth dimensional light source. Let’s use a transparent tesseract which has all its edges in dark color, and we could count 32 edges. (A square has four edges, a cube has 12 edges, and a tesseract has 32 edges)
The mathematical progression of edges is not so neatly accomplished; in fact you need to disregard using that method. But, we can use the same process up to a point. When we were going from an object of any dimension to the object of the next dimension, we used the object of that dimension as a base, unfolded the sides 90°, and added a mirror image of the base at a top. So, for a tesseract, we will do the same thing. We will use a cube as a base, and use a cube as the cap. Then we will connect all of the corners of the base cube with its corresponding corner in the cap cube. That means eight connecting lines. (Here I am doing to you the reader, just what I wrote that I hated when it was done to me. But, I tried to warn you that you might be approaching insanity if you went on.)
Which means that in order to count the number of edges of the figure in any dimension, we will start with the number of edges of that figure in the previous dimension times two, (we used the figure twice, once at the base and once at the top) plus the number of lines drawn from corner to corner from the figure used as the base to the mirror image used as the top. The mathematical progression mainly lies in the number of lines drawn between the two figures.
From a line to a square, there are two lines drawn; from a square to a cube there are four lines drawn; and from a cube to a tesseract there eight lines drawn. That means that from a tesseract to a hypertesseract (fifth dimension) there would be 16 lines drawn and since a tesseract has 32 edges, we take that number times two which gives us 64 and add the number of lines (16) and we get 80 which is the number of edges in a hypertesseract, that is if anybody cares to know, because I am sure it will come up in everyday conversation if you just pay attention. (All you need do is wait for the right moment in the conversation, and then you pounce, saying “and by the way, did you know a hypertesseract has 80 edges.” This is sure to win you great esteem and a number of admirers. Just watch the looks you get from others.)
So now let’s do the progression.
⦁ A one dimension line has one edge.
⦁ A two dimension square has four edges.
⦁ A three dimension cube has 12 edges.
⦁ A four dimension tesseract has 32 edges.
And if anybody gives a damn
A fifth dimension hyper tesseract has 80 edges. (32 edges of a tesseract times two = 64, plus the 16 connecting lines between the corners of the tesseract base and the mirror image tesseract top=80)
So now that we know all this stuff about a tesseract, what does a tesseract look like? Naturally that is not a very intelligent question since we cannot know the appearance of a fourth dimension object, no matter how much information we have on that object. But we can make a three dimension attempt to comprehend something of its makeup.
The following hyphens are used so that each set of hyphenated words equals one diagram.
It is very important to remember that two-mirror-image-one-dimensional-finite-lines separated at their corners by two-other-mirror-image-finite-lines equals a two dimensional square. —–And, two-mirror-image-two- dimensional-squares separated at their corners by four-other-mirror-image- squares, or four lines, equals a three dimensional cube.—– And, two-mirror- image-three-dimensional-cubes separated at their corners by six-other- mirror-image-cubes, or eight lines, equals a tesseract. (I’m not stupid, I know you just skim read this red stuff, but I am going to put it on paper so that it is easier. AND for those of you that instantly understand what it took me years to figure out, I ADMIRE YOUR ABILITY.) So, we must have those two cubes connected at their eight corners (Each cube having eight corners, and there are two cubes).
Also, we must remember, in a two dimensional square there are two lines converging at the corners. In a three dimensional cube there are three lines converging at the corners. In a four dimensional tesseract there are four lines converging at the corners.
IMAGES OF THE EIGHT SIDES OF A TESSERACT AS THEY APPEAR ON TWO DIMENSIONAL DRAWINGS
In order to better comprehend the following diagrams of the eight sides of a tesseract, we are first going to take a brief look at the complete tesseract diagram. Remember this is a two dimensional diagram of a three dimensional shadow of a fourth dimensional tesseract. In a computer can be found several various diagrams of tesseracts, but most of them show tesseracts sides of these objects with sides which are diminishing in size. When you hold a di, it has six sides , all of the same size. The following diagram can easily be made to show all eight sides of the tesseract with sides of the same size. We have, however chosen to elongate it to better show the different sides.
What you see is each one of the eight sides is made of the six sides of our three dimensional cube. (It seems weird, but our cubes seem just as weird to a two dimensional creature.) There is a cube shaped side on each of the two sides of the tesseract; a cube shaped side on both the top and bottom of the tesseract (making a total of four sides); a cube shaped side on each end of the tesseract, (making six sides; and finally cube shaped sides extending both ways thru the middle of the tesseract, making eight four dimensional side, each side consisting of six three dimensional sides.
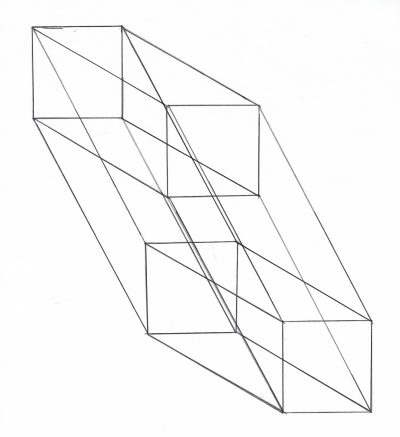
So we must meet these criteria. Let’s look at figure one. There are the two cubes separated by eight lines, and every corner has four lines converging between corresponding corners.

In figure one: the first six sided cube is connected to the second six sided cube, creating two sides of our eight-sided .tesseract
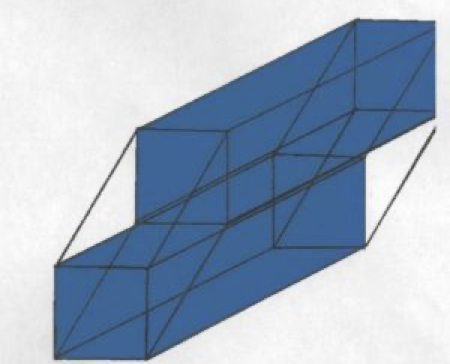
In figure two the top six sided cube is connected to the bottom six sided cube,
creating two more sides of our eight sided tesseract
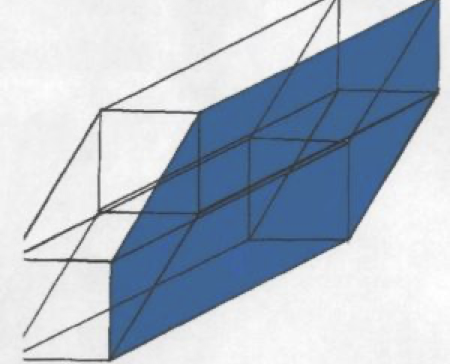
Figure three shows the corners of the right six sided cube connected to the corners of the right side of the second six sided cube, creating one more side of our eight sided tesseract We now have five of our eight sides.

Figure four shows the corners of the left six sided cube connected to the corners of the left side of the corners of the second cube, creating one more side of our eight sided tesseract. We now have six of our eight sides
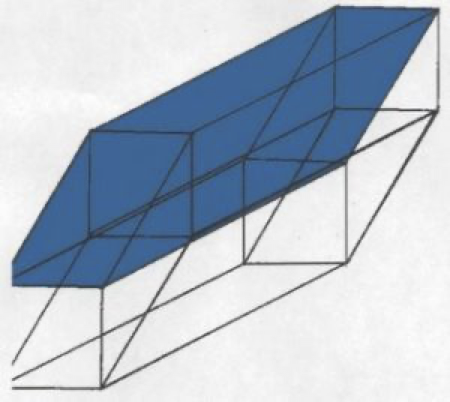
Figure five shows the corners of the top six sided cube connected to the corners of the top of the corners of the second cube, creating one more side of our eight sided tesseract . We now have seven of our eight sides.
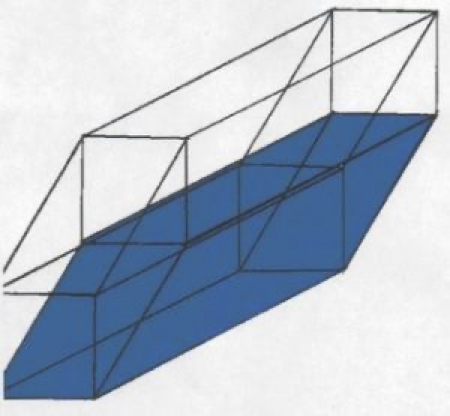
Figure six shows the corners of the bottom six sided cube connected to the corners of the bottom of the corners of the second cube, creating one more side of our eight sided tesseract. We now have eight of our eight sides.
Hoorah for our team!!!
PLEASE NOTE:
IN THIS PAPER, ALL CAPITAL LETTERS AND COLORED INK ARE USED TO INDICATE TO THE READER SOMETHING I THINK IS IMPORTANT. IT IS ALSO AN ATTEMPT TO BREAK UP THE MONOTONY OF THE ORDINARY PRINTED PAGE FOR THE READER. IT IS NOT AN ATTEMPT TO HOLLER AT THE READER.